Numerical analysis solutions manuals are essential resources for understanding numerical methods. They provide detailed solutions to textbook problems, covering topics like root-finding and interpolation, aiding students in mastering complex concepts.
1.1 Overview of Numerical Analysis and Its Importance
Numerical analysis is a field of mathematics focused on solving numerical and mathematical problems using computational methods. It is essential for engineering, physics, and computer science, providing approximate solutions to complex equations. Numerical methods are widely used in simulations, data analysis, and algorithm development. This field enhances problem-solving efficiency and accuracy, making it a cornerstone of scientific and technological advancements.
1.2 Role of Solutions Manuals in Numerical Analysis
Solutions manuals play a crucial role in numerical analysis by providing step-by-step explanations and answers to textbook problems. They help students verify their work, understand complex methods, and improve problem-solving skills. These manuals also serve as valuable references for instructors, ensuring consistent and accurate solutions. Accessible online, they offer a convenient resource for mastering numerical techniques and algorithms, enhancing both teaching and learning experiences in the field.
1.3 Popular Numerical Analysis Textbooks and Their Solutions Manuals
Popular numerical analysis textbooks include works by Timothy Sauer, Burden, and Faires, each accompanied by detailed solutions manuals. These manuals provide step-by-step solutions to exercises, enhancing understanding of numerical methods. Widely used, they are available in PDF formats online, offering convenient access for students and educators. Their comprehensive coverage of topics like root-finding and interpolation makes them indispensable resources for learning and teaching numerical analysis effectively.

Timothy Sauer Numerical Analysis Solutions Manual
The Timothy Sauer Numerical Analysis Solutions Manual is a supplementary guide for his textbook, providing detailed solutions to exercises. It offers step-by-step explanations for numerical methods, including interpolation and integration, helping students verify answers and understand problem-solving strategies. Available in PDF format, it is a valuable resource for learners seeking to master numerical analysis concepts effectively.
2.1 Features of the Timothy Sauer Solutions Manual
The Timothy Sauer Solutions Manual offers detailed step-by-step solutions to exercises, covering numerical methods like interpolation and integration. It provides clear explanations, enabling students to understand problem-solving strategies. Available in PDF format, it includes worked-out examples for complex topics, making it an invaluable resource for learners seeking to master numerical analysis effectively. Its structured approach ensures comprehensive understanding of key concepts and methodologies.
2.2 How to Use the Manual for Effective Learning
To use the Timothy Sauer Solutions Manual effectively, start by referencing it alongside the textbook. Review the detailed step-by-step solutions to verify your answers and understand problem-solving strategies. Focus on understanding the methodology behind each solution rather than just the final result. Practice solving problems independently before consulting the manual, and use it to identify areas where you need more review. This approach enhances learning and mastery of numerical analysis concepts.
2.3 Key Topics Covered in the Manual
The Timothy Sauer Solutions Manual covers essential numerical analysis topics, including root-finding methods, interpolation, and numerical integration. It provides detailed solutions for linear systems and matrix algebra, ensuring a comprehensive understanding of numerical methods. The manual also addresses error analysis and iterative techniques, offering practical insights into solving real-world problems. These topics are presented with clear, step-by-step explanations, making the manual an invaluable resource for students and professionals alike.
Burden and Faires Numerical Analysis Solutions Manual
The Burden and Faires Solutions Manual offers detailed solutions for numerical analysis problems, covering methods like interpolation and linear systems. It supports the 9th and 10th editions, aiding students and professionals in mastering numerical techniques effectively.
3.1 Overview of the 9th and 10th Editions
The 9th and 10th editions of Burden and Faires’ Numerical Analysis Solutions Manual provide comprehensive solutions to exercises, covering numerical methods, interpolation, and linear systems. The 9th edition focuses on core numerical techniques, while the 10th introduces modern computational tools. Both editions are designed to enhance understanding and problem-solving skills, offering detailed step-by-step explanations for students and professionals alike.
3.2 Detailed Solutions to Exercises
The Burden and Faires solutions manual offers detailed step-by-step solutions to exercises, covering numerical methods like interpolation, integration, and root-finding. Each solution explains the methodology, ensuring students understand both the process and final answer. This resource is invaluable for self-study and homework verification, providing clarity on complex numerical techniques and enhancing problem-solving skills effectively.
3.3 Coverage of Numerical Methods and Algorithms
The Burden and Faires solutions manual comprehensively covers numerical methods and algorithms, including interpolation, numerical integration, and solving linear systems. It provides in-depth explanations of error analysis and algorithm stability, ensuring a thorough understanding of numerical techniques. This resource is tailored for students and professionals, offering practical insights into implementing and analyzing numerical solutions effectively across various engineering and scientific applications.
Solutions for Specific Numerical Methods
Numerical analysis solutions manuals offer detailed guidance for specific methods like root-finding, interpolation, and numerical integration. They provide step-by-step solutions, ensuring clarity and understanding of complex techniques.
4.1 Solutions for Root-Finding Methods
Root-finding methods, such as the Bisection Method and Newton’s Method, are fundamental in numerical analysis. Solutions manuals provide detailed steps for solving equations, ensuring accuracy and understanding. These methods are crucial for identifying roots of complex functions, often encountered in engineering and science. By following the solutions, students can master iterative techniques and error analysis, essential for practical applications.
4.2 Solutions for Interpolation and Approximation
Interpolation and approximation methods are crucial for estimating functions from data points. Solutions manuals provide detailed steps for techniques like Lagrange and Newton polynomials, enabling accurate function representation; These methods are vital in data analysis, engineering, and scientific simulations. By mastering these solutions, students can effectively approximate complex functions and understand error bounds, enhancing their problem-solving skills in numerical analysis.
4.3 Solutions for Numerical Integration
Numerical integration solutions provide methods for approximating definite integrals when analytical solutions are difficult. Techniques like the Trapezoidal Rule and Simpson’s Rule are detailed in manuals, offering step-by-step guidance. These methods are essential for engineering and scientific applications, ensuring accurate results. Solutions manuals also cover error analysis and adaptive algorithms, helping students understand how to balance accuracy and computational efficiency in real-world problem-solving scenarios.
4.4 Solutions for Linear Systems and Matrix Algebra
Numerical solutions for linear systems and matrix algebra are crucial in solving real-world problems. Manuals provide detailed methods like Gaussian Elimination and LU Decomposition, ensuring accuracy. They cover matrix operations, eigenvalue problems, and error analysis. These solutions help students understand stability and computational efficiency, essential for engineering and scientific applications. Step-by-step explanations in manuals make complex concepts accessible, aiding in mastering numerical methods effectively.

Error Analysis in Numerical Solutions
Error analysis is crucial for understanding precision in numerical methods. It identifies error types, propagation, and stability, ensuring reliable solutions by minimizing computational inaccuracies effectively.
5.1 Understanding Error Types in Numerical Methods
Numerical methods introduce errors due to approximations and limitations in computation. Rounding errors occur from finite precision, while truncation errors arise from method approximations. Understanding these error types is crucial for assessing solution accuracy and developing strategies to minimize their impact. By analyzing error sources, such as computational steps or algorithmic approximations, users can better evaluate the reliability of numerical solutions and improve computational outcomes effectively.
5.2 Error Propagation and Stability
Error propagation refers to how errors accumulate during computations, impacting final results. Stability determines whether errors grow or diminish as computations progress. In stable methods, small errors remain manageable, while unstable methods amplify them. Understanding error propagation is vital for assessing the reliability of numerical solutions. Techniques like rounding error analysis and stability tests help identify robust methods, ensuring accurate and dependable outcomes in numerical analysis applications.

5.3 Strategies for Minimizing Errors
To minimize errors in numerical analysis, strategies like refining grid sizes, using iterative refinement, and applying high-precision arithmetic are essential. Iterative methods often include techniques to reduce residual errors, while error-correcting algorithms help maintain accuracy. Regularly verifying solutions against known cases and leveraging stable numerical methods further enhance reliability. These approaches, detailed in solutions manuals, ensure computations remain accurate and trustworthy, addressing both rounding and truncation errors effectively.
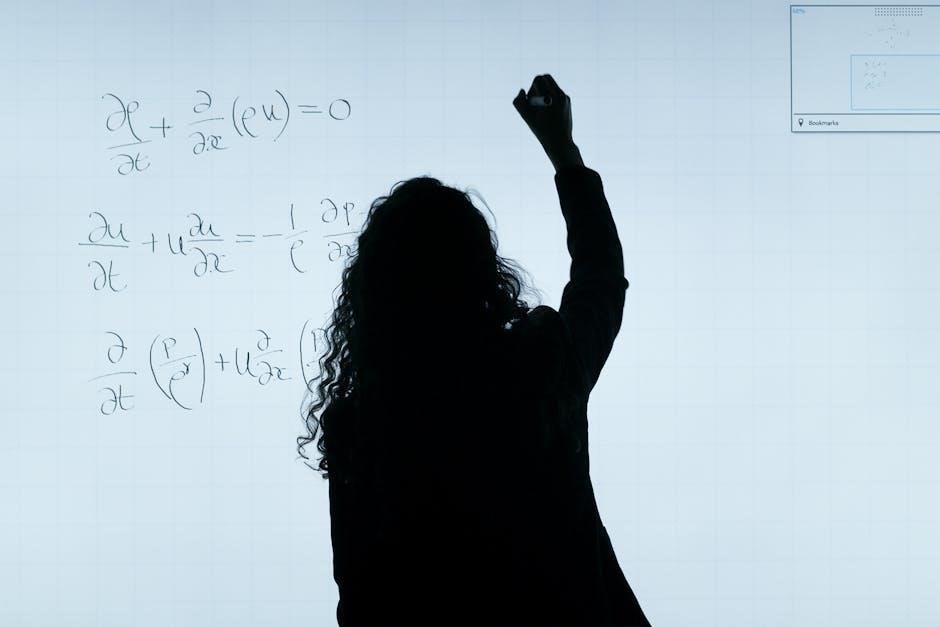
Computational Tools for Numerical Analysis
Computational tools like MATLAB and Python are essential for numerical analysis, offering robust libraries for algorithm implementation and data visualization, enhancing problem-solving efficiency and accuracy significantly.
6.1 Role of MATLAB in Numerical Analysis
MATLAB is a powerful tool for numerical analysis, offering built-in functions for various numerical methods. It enables efficient algorithm implementation, data visualization, and simulation. Widely used in both education and research, MATLAB simplifies complex computations, making it easier to explore numerical solutions. Its interactive environment and extensive libraries support tasks like root-finding, interpolation, and linear algebra, providing students and professionals with a robust platform for problem-solving and analysis.
6.2 Using Python for Numerical Computations
Python is a powerful tool for numerical computations, offering libraries like NumPy and SciPy. These libraries provide efficient methods for tasks such as interpolation, integration, and linear algebra. Python’s simplicity and flexibility make it ideal for numerical analysis, enabling users to implement algorithms and visualize data effectively. It supports both educational and professional applications, making it a versatile choice for numerical problem-solving.
6.3 Software Packages for Numerical Solutions
Software packages like MATLAB, Mathematica, and SciPy are indispensable for numerical solutions. They offer built-in functions for interpolation, integration, and linear algebra, enhancing computational efficiency. These tools provide visualization capabilities, enabling users to interpret results effectively. They are widely used in academia and industry for solving complex numerical problems, ensuring accuracy and reliability in simulations and analyses.

Accessing Numerical Analysis Solutions Manuals Online
Numerical analysis solutions manuals are widely available online through platforms like Vaia, StudySoup, and Chegg. These resources offer step-by-step solutions, homework answers, and study guides for various textbooks.
7.1 Popular Platforms for Solutions Manuals
Popular platforms like Vaia, StudySoup, and Chegg offer extensive collections of numerical analysis solutions manuals. These platforms provide access to step-by-step solutions, homework answers, and study guides for various textbooks, including Burden and Faires’ 9th and 10th editions. Additionally, Cengage Learning and other educational websites offer digital solutions manuals, enabling students to access resources conveniently. These platforms cater to diverse learning needs, ensuring comprehensive support for numerical analysis studies.
7.2 How to Find Reliable Online Resources
To find reliable online resources for numerical analysis solutions, start by exploring platforms like Vaia, StudySoup, and Chegg, which offer verified solutions. Additionally, check the official websites of textbook publishers, as they often provide companion manuals. University libraries and course portals may also host trusted materials. Always verify the source’s credibility and ensure the solutions align with your textbook edition for accuracy and relevance to your studies.
7.3 Benefits of Digital Solutions Manuals
Digital solutions manuals offer unparalleled convenience and accessibility. They provide instant access to step-by-step solutions, reducing the need for physical copies. Features like search functionality, interactive tools, and mobile access enhance learning efficiency. Platforms such as Vaia and StudySoup also offer additional resources like flashcards and AI-driven study aids, making digital manuals indispensable for modern students seeking to master numerical analysis effectively.

Applications of Numerical Analysis Solutions
Numerical analysis solutions are widely applied in engineering, scientific simulations, and real-world problem-solving. They enable accurate modeling, optimization, and prediction in fields like physics, chemistry, and data science.
8.1 Engineering Applications
Numerical analysis plays a crucial role in engineering, enabling the simulation and modeling of complex systems. It is used in structural analysis, heat transfer, fluid dynamics, and signal processing. Engineers rely on numerical methods to optimize designs, predict system behavior, and solve real-world problems efficiently. These solutions enhance accuracy and reduce costs, making them indispensable in modern engineering practices.
8.2 Scientific Simulations
Numerical analysis is fundamental to scientific simulations, enabling researchers to model complex phenomena like fluid dynamics, climate patterns, and molecular interactions. These simulations rely on numerical methods to solve differential equations and predict system behaviors. By providing accurate and efficient solutions, numerical analysis drives advancements in physics, chemistry, and biology, allowing scientists to explore scenarios that are difficult or impossible to study experimentally.
8.3 Real-World Problem Solving
Numerical analysis solutions manuals are invaluable for tackling real-world problems in engineering, economics, and physics. They provide step-by-step guidance for solving practical issues like optimization, fluid dynamics, and data analysis. By offering clear explanations and solutions, these manuals empower professionals and students to apply numerical methods effectively, ensuring accurate and efficient problem-solving in diverse industries and academic disciplines.
Future Trends in Numerical Analysis Solutions
Numerical analysis solutions are evolving with advancements in AI and machine learning. Future trends include enhanced computational methods, integration of big data, and emerging applications in diverse fields.
9.1 Advances in Computational Methods
Advances in computational methods are revolutionizing numerical analysis. High-performance computing and machine learning integrate with traditional algorithms, enhancing accuracy and efficiency. AI-driven tools optimize problem-solving, while adaptive methods improve error reduction. These innovations enable faster, more precise simulations, addressing complex challenges in engineering and science. The fusion of computational techniques with numerical analysis ensures robust solutions for real-world applications, driving progress in various fields.
9.2 Integration of AI in Numerical Analysis
The integration of AI in numerical analysis is transforming problem-solving. Machine learning algorithms optimize numerical methods, improving accuracy and efficiency. AI enhances error reduction, adaptive meshing, and complex equation solving. By automating iterative processes, AI accelerates simulations, enabling real-time solutions. This synergy between numerical analysis and AI fosters innovation, addressing intricate challenges in science and engineering with unprecedented precision and speed.
9.3 Emerging Applications and Challenges
Numerical analysis solutions are advancing in climate modeling, fluid dynamics, and AI-driven simulations. Emerging applications include tsunami propagation models and multibody dynamics. However, challenges like high-performance computing demands and complex data integration persist. Researchers focus on developing more accurate and efficient algorithms to address these issues, ensuring numerical solutions remain reliable and adaptable to evolving scientific and engineering needs.
Numerical analysis solutions manuals are invaluable for mastering complex numerical methods. They provide clear solutions, enhance understanding, and serve as essential tools for both students and professionals.
10.1 Summary of Key Points
Numerical analysis solutions manuals are indispensable tools for mastering numerical methods. They provide detailed solutions to exercises, enhancing understanding of concepts like root-finding and interpolation. These manuals cater to both students and professionals, offering step-by-step explanations and practical applications. By bridging theory and practice, they facilitate problem-solving in engineering, scientific simulations, and real-world scenarios, ensuring accurate and efficient numerical computations.

10.2 Importance of Solutions Manuals in Learning
Solutions manuals are vital for effective learning in numerical analysis. They provide clear, step-by-step explanations, enabling students to verify their work and grasp complex concepts. These resources bridge the gap between theory and practice, reinforcing understanding through practical examples. By offering detailed solutions, they empower learners to improve problem-solving skills, build confidence, and master numerical methods efficiently, making them indispensable for academic and professional success.
10.3 Final Thoughts on Numerical Analysis Solutions
Numerical analysis solutions manuals are indispensable tools for mastering numerical methods. They offer comprehensive, step-by-step guidance, enhancing understanding and problem-solving skills. By providing detailed explanations and practical examples, these resources empower learners to tackle complex challenges confidently. Their accessibility and thorough coverage make them essential for both academic and professional success, ensuring a strong foundation in numerical analysis for future endeavors.

References and Further Reading
Numerical analysis solutions manuals are supported by textbooks like Burden, Faires, and Sauer. Online platforms such as Vaia offer extensive resources and step-by-step solutions for reference.
11.1 Recommended Textbooks
provide step-by-step solutions for homework problems. Platforms such as Vaia and StudySoup also offer access to verified solutions for these textbooks, enhancing learning and problem-solving skills. The SIAM Journal on Numerical Analysis is a valuable resource for advanced research.
11.2 Online Resources
Online platforms like Vaia and StudySoup offer extensive numerical analysis solutions, including step-by-step explanations and flashcards. Websites such as Chegg Study and Course Hero provide access to solved problems and study guides. Additionally, resources like SIAM Journal on Numerical Analysis and university lecture notes are valuable for advanced topics. These online tools support learning and problem-solving, making them indispensable for students and researchers alike.
11.3 Research Articles and Journals
Research articles and journals like the SIAM Journal on Numerical Analysis offer in-depth insights into numerical methods. They publish studies on error analysis, polynomial interpolation, and multibody dynamics. Journals provide access to cutting-edge research, enabling scholars to explore advanced topics. These resources are invaluable for understanding theoretical foundations and practical applications, supporting both academic and professional advancements in numerical analysis.

